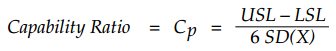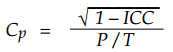Using the Precision to Tolerance Ratio - مجله خبری کنترل کیفیت

The usual motivation behind the computation of the P/T ratio is a desire to determine if a measurement procedure is adequate for a given production process. And there are two ways that measurements support a production process: They can be used to scrape the burnt toast (inspection), or they can be used to learn how to stop burning the toast (process improvement). If the measurement system is adequate to allow us to improve the process, then we can often get to the point where we no longer have to depend upon inspection to ship conforming product. So of these two ways that measurements support production, the role of process improvement is the more critical in the long term.

Will the measurements support process improvement?

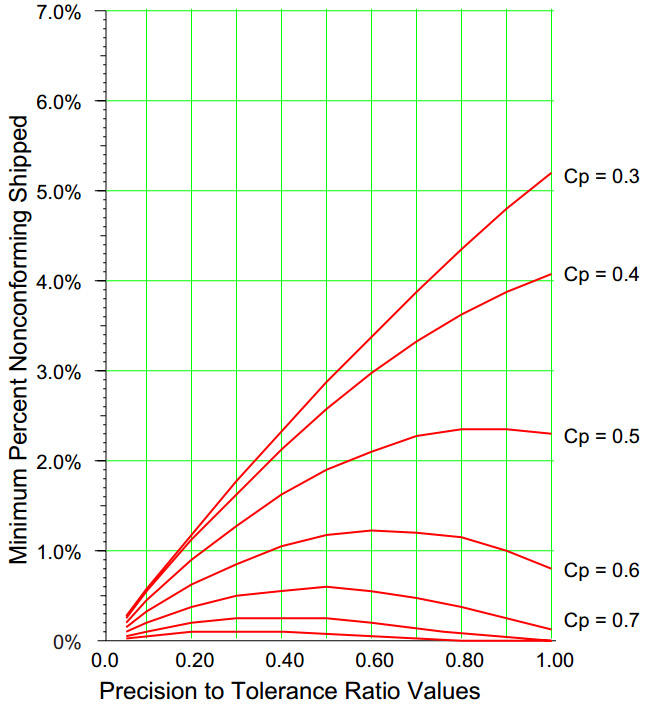
Figure 7: Minimum percentages of nonconforming product shipped

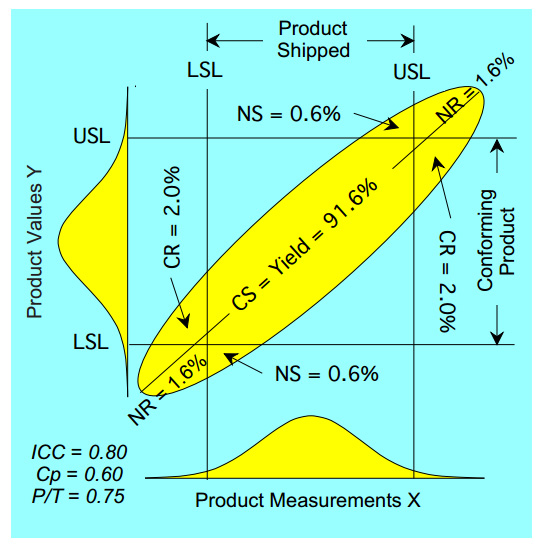
The product measurements, X, will consist of the product values, Y, plus measurement errors, E. The relationship between X and Y may be modeled with a bivariate normal distribution. The ellipse in figure 6 shows the three-sigma contour of a bivariate normal distribution having an ICC value of 0.80 and a capability ratio of 0.60.

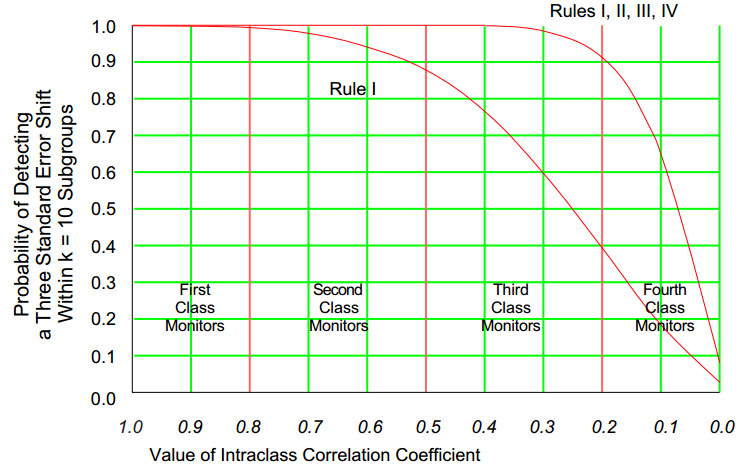
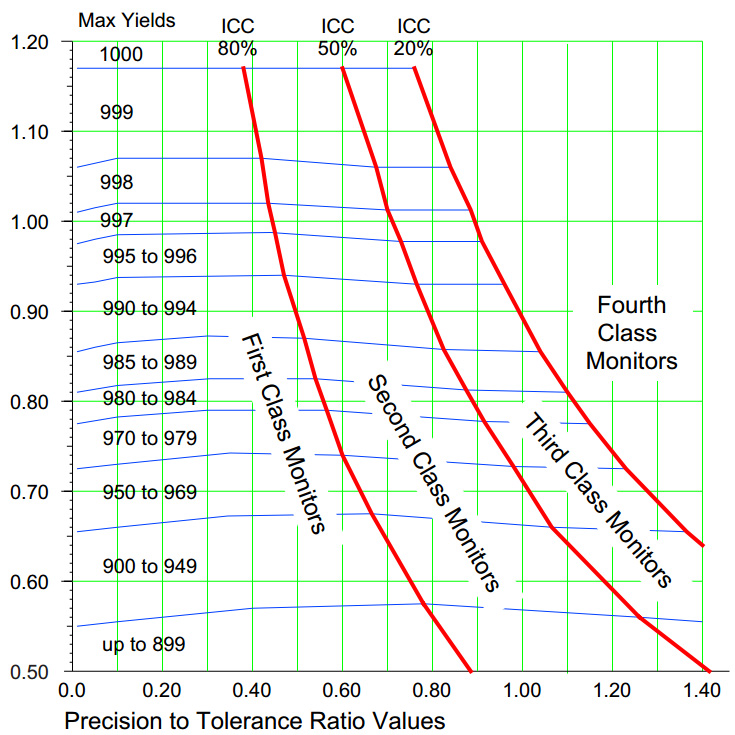
When the ICC falls below 0.20, the measurements contain very little information about the product. These fourth-class monitors are essentially useless for process improvement.

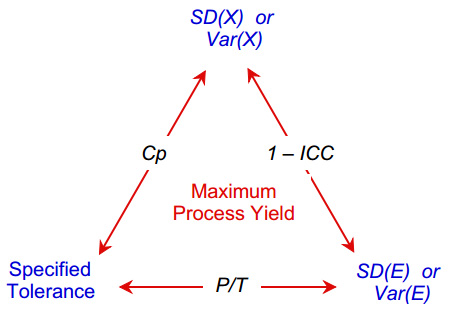
Three ratios are commonly used to compare the quantities on the corners of the triangle. The capability ratio, Cp, compares the specified tolerance with the (within subgroup) standard deviation of the product measurements:

So please consider turning off your ad blocker for our site.

The following is provided for those interested in duplicating the results shown in the graphs. The relationship between the product values, Y, and the product measurements, X, can be modeled using a bivariate normal distribution as shown in figure 6. In this model, the minor axis of the ellipse is a function of the measurement error.

These ratios are related in the manner shown by the following equation. This means that knowledge of any two of these ratios will completely define the third.

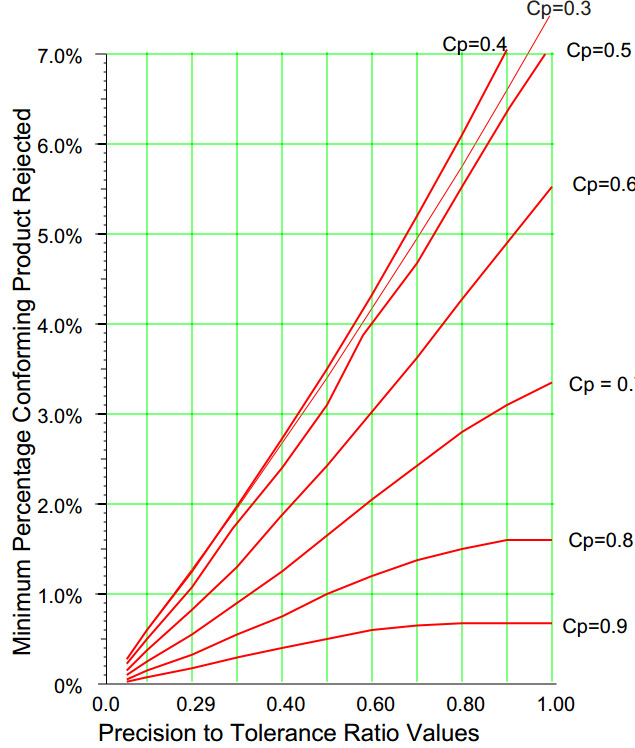
Figure 8: Minimum percentages of conforming product rejected

The maximum process yield depends upon three quantities: the specified tolerance; the variation in the measurement process, SD(E); and the variation in the stream of product measurements, SD(X).

The precision to tolerance ratio compares the standard deviation of the measurement process with the specified tolerance.

For example, if your P/T ratio is 0.60 and your capability ratio is 0.80, your process will have a maximum process yield of about 980 ppt. Operating predictably and on-target will result in about 980 conforming units shipped per thousand units produced. Operating at less than full potential will result in a lower yield.

Inspection places a premium on having a good measurement system. When a process is operated unpredictably or off target, the misclassifications will increase beyond the minimums given above. The costs of improving the measurement system, plus the costs of inspection, rework, and scrap, will lower productivity without increasing the quality of the product shipped. I have had clients who were so comfortable with inspection that they put on more inspectors, increased the size of the rework department, and slowly went out of business.

The proportion of conforming product (C) that gets rejected (R) by the specifications will be approximated by the volume under the bivariate model in the regions labeled CR. This is a misclassification that occurs due to measurement error.

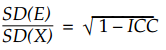
The proportion of nonconforming product (N) that gets rejected (R) by the specifications will be approximated by the volume under the bivariate model in the regions labeled NR.

Without loss of generality we may assume:

For the role of process improvement, we need a measurement system that allows us to detect those changes in our process that are large enough to be of economic impact. To see how a measurement system affects the ability of a process behavior chart to detect process changes, we will use the intraclass correlation coefficient.

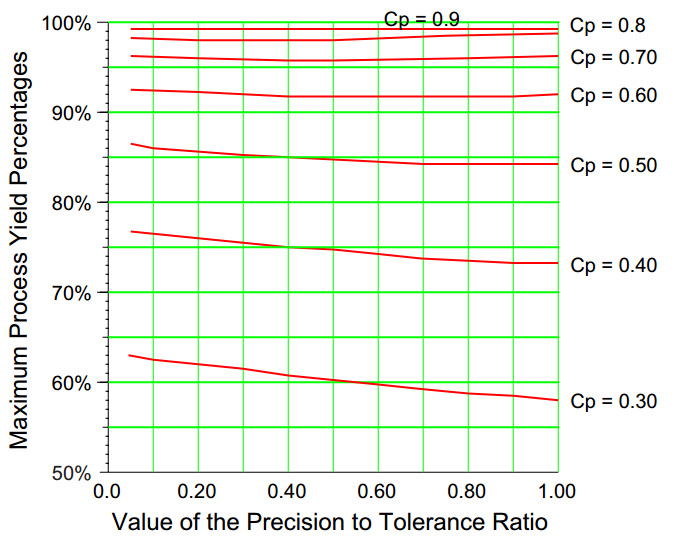
Figure 3 shows the information of figure 2 in a different format and extends the coverage to lower capability ratios. Here each curve represents a fixed value for the capability ratio while the maximum process yields are shown on the vertical axis.

When a production process is not operated on-target, or when it is not operated predictably, it is not being operated up to its full potential. And when a process is not operated up to its full potential, then its actual yield will be less than the maximum process yield. Yet here the maximum process yield may still be used as a conservative estimate of the hypothetical process potential; it will give us an idea of what the process yield could be when operated up to its full potential.

So, the P/T ratio does not limit the maximum process yields. Neither does it characterize the relative usefulness of the measurements for keeping process behavior charts. But does it tell us anything about using the measurements to scrape the burnt toast?

Inspection

With appropriate changes in the limits of integration, we can use the equation above to find volumes for the regions CR, NS, and NR for any given combination of the P/T and capability ratios.

When the intraclass correlation is greater than 0.80, the measurement system is a first-class monitor for that production process. A process behavior chart using detection Rule 1 alone has better than a 99% chance of detecting a three-standard error shift.

Figure 8 shows the minimum percentage of conforming product that will get rejected for a given capability and P/T ratio when the process is operated up to its full potential.

However, someone has to pay for this content. And that’s where advertising comes in. Most people consider ads a nuisance, but they do serve a useful function besides allowing media companies to stay afloat. They keep you aware of new products and services relevant to your industry. All ads in Quality Digest apply directly to products and services that most of our readers need. You won’t see automobile or health supplement ads.

Our PROMISE: Quality Digest only displays static ads that never overlay or cover up content. They never get in your way. They are there for you to read, or not.

Using published tables of the power functions for process behavior charts, we can compute the probabilities of detecting various sized shifts for various values of the intraclass correlation. Here we shall consider detecting a three-standard-error shift within ten subgroups of when that shift occurs. Figure 4 shows two curves: The lower curve is for the use of detection rule one alone, while the upper is for the use of all four Western Electric zone tests. The interesting thing about both curves is how slowly they drop off as the intraclass correlation goes to zero.

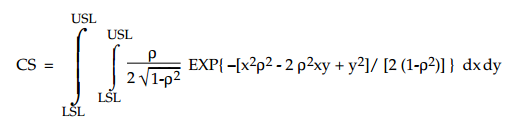
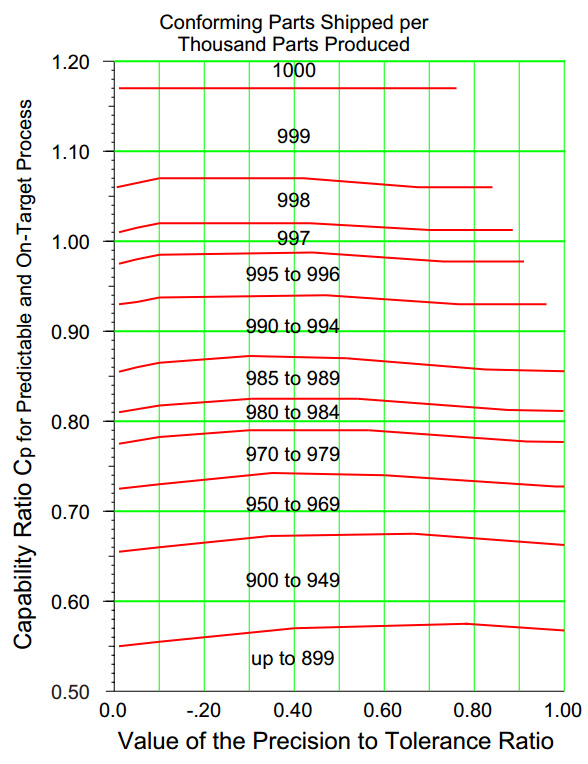
Figure 2: How maximum process yields change with P/T and capability

Then, for a given P/T ratio and a given capability ratio, we may find the ICC value and compute the maximum process yield by integrating the resulting bivariate normal distribution with respect to both X and Y over the region labeled CS (i.e., between the specification limits).

Quality Digest does not charge readers for its content. We believe that industry news is important for you to do your job, and Quality Digest supports businesses of all types.

As we learned last month, the precision to tolerance ratio is a trigonometric function multiplied by a scalar constant. This means that it should never be interpreted as a proportion or percentage. Yet the simple P/T ratio is being used, and misunderstood, all over the world. So how can we properly make use of the P/T ratio?

So that the ratio of SD(E) to SD(X) will be given by:

Thanks,
Quality Digest

Using the Precision to Tolerance Ratio

What does this ratio tell us?

The region labeled CS represents the maximum process yield. As the capability ratio increases, the specifications get wider relative to the ellipse and more of the ellipse will fall within the specification square. As Var(E) gets smaller, the ellipse gets narrower and the minor axis shrinks.

When we use probability models to characterize what to expect in practice, we should round off the results to parts per thousand. No probability model will ever describe reality out to parts per ten-thousand or beyond. While we may compute values out to more decimal places, and while the extra digits may be necessary for precise computations, these extra digits are meaningless when it comes to describing finite processes.

The proportion of conforming product (C) that gets shipped (S) will be approximated by the volume under the bivariate model in the region labeled CS. This value will be the maximum process yield.

Figure 1: The maximum process yield depends upon three quantities

When the intraclass correlation is between 0.50 and 0.20, the measurement system is a third-class monitor for that production process. Here a process behavior chart using all four detection rules still has better than a 91% chance of detecting a three-standard error shift in the production process within ten subgroups.

So if you’re concerned with the value of your P/T ratio, you may not have progressed to the point of asking the right questions. The choice is yours. Are you going to continue to scrape the burnt toast, or are you going to learn how to stop burning the toast?

Appendix: Finding the maximum process yields

Figure 4: The ability to detect economic changes

Figure 6: Relationship between X and Y when ICC = 0.80

When sorting nonconforming product from conforming product we will want perfect measurements. Any amount of measurement error will create the possibility of misclassifications where some conforming product gets rejected and some nonconforming product gets shipped. To illustrate how this happens, we return to the model for our measurements.

So while none of these three ratios will tell the whole story by itself, any two of them may be used to determine the maximum process yield. Figure 2 shows how the P/T ratio and the capability ratio combine to determine the maximum process yield. The horizontal axis shows values of the P/T ratio ranging from 0.00 to 1.00, while the vertical axis shows capability ratios ranging from 0.50 to 1.20. The values in the graph are the maximum process yields, in parts per thousand. These are the number of conforming units shipped per thousand units produced.

The flatness of the curves in figures 2 and 3 shows that the P/T ratio has very little impact upon maximum process yields. The yields are almost completely determined by the capability ratios. So, we don’t have to have a small P/T ratio in order to have a high maximum process yield. We can have very high yields even with a large P/T ratio. This means that knowing the P/T ratio doesn’t tell us anything useful about the maximum process yield.

The usefulness of the measurement system

Figure 5: P/T does not determine ICC

When the intraclass correlation is between 0.80 and 0.50, the measurement system is a second-class monitor for that production process. Here a process behavior chart using detection Rule 1 alone will have better than an 88% chance of detecting a three-standard error shift. Using all four detection rules together gives a 100% chance of detecting a three-standard error shift within ten subgroups.

And the intraclass correlation coefficient (ICC) defines that proportion of the variation in the stream of product measurements, Var(X), that can be directly attributed to the variation in the product steam, Var(Y):

And the proportion of nonconforming product (N) that gets shipped (S) will be approximated by the volume under the bivariate model in the regions labeled NS. This is the other misclassification that occurs due to measurement error.

The regions labeled CR and NS represent misclassifications due to measurement error. CR represents conforming product that gets rejected, while NS represents nonconforming product that gets shipped. By integrating the bivariate normal distribution over the regions shown, we can estimate the minimum percentages for each type of misclassification. Figures 7 and 8 show these minimums as a function of the capability ratio and the P/T ratio.

and Bivariate Correlation =

Figure 5 is an extension of figure 2 showing the curves that separate these four classes of monitors. While P/T ratios below 0.30 will correspond to first-class monitors, larger P/T ratios may correspond to various classes of monitors. Since first-, second-, and third-class monitors are all useful for process improvement, the P/T ratio does not describe the relative utility of a measurement process.

Figure 7 shows the minimum percentage of nonconforming product that will get shipped for a given capability and P/T ratio when the process is operated up to its full potential. (The bottom two curves are for capabilities of 0.80 and 0.90.)

The only way to avoid these misclassifications is to have a capability ratio large enough for the ellipse to fit within the square, or to have zero measurement error. So, if you depend upon inspection in order to ship conforming product, your target value for the P/T ratio has to be zero.

Summary

To assess the adequacy of the measurement process for the role of process improvement, we use the maximum process yield. This is that fraction of the product produced that is both conforming and gets shipped when the production process is operated predictably and on target.

Published: Monday, September 4, 2023 – 12:03