Using Stress/Strength Analysis to Reduce Sample Size

A good resource to follow up on this is Wayne Taylor’s book Statistical Procedures for the Medical Device Industry (Taylor Enterprises, 2017), in which Taylor notes that:

Oftentimes, due to several constraints such as material availability, resource constraints, and unforeseen circumstances, one may not be able to use the required sample sizes. I’m proposing here that we can use the stress/strength relationship to appropriately justify the use of a smaller sample size, while at the same time not compromising on the desired reliability/confidence level combination.

Published: Monday, October 16, 2023 – 12:03

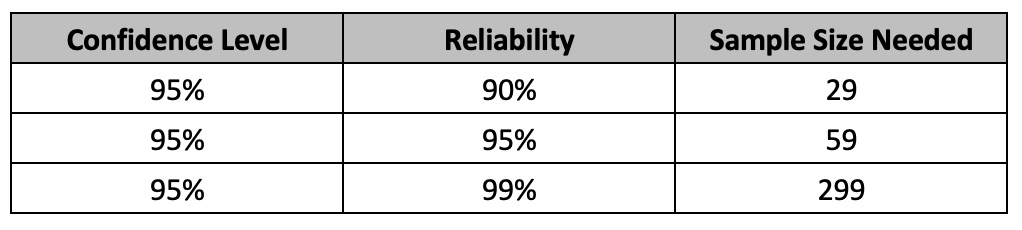
this equates to 59 samples. Similarly for 2x stress conditions, we estimate 2% failures, and here R = 0.98. Using C = 0.95 in the equation, we get the sample size required as 149.

Our PROMISE: Quality Digest only displays static ads that never overlay or cover up content. They never get in your way. They are there for you to read, or not.

Following this logic, if we increase the testing stress, we will also increase the likelihood for failures. For example, by increasing the stress five-fold (7.5 lbf), we are also increasing the likelihood of failure by five-fold (5%) or more. Therefore, if we test 60 parts (one-fifth of 299 from the original study) at 7.5 lbf and see no failures, this would equate to 99% reliability at 95% confidence at 1.5 lbf. We can claim at least 99% reliability of performance at 95% confidence level during normal use of product. We were able to reduce the sample size needed to demonstrate the required 99% reliability at 95% confidence level by increasing the stress test condition.

“Many test methods contained in standards are in fact stress tests designed to provide a safety margin. For example, the ASTM packaging standards provide for conditioning units by repeated temperature/humidity cycles and dropping of units from heights that are more extreme and at intervals that are more frequent than most products would typically see during shipping. As a result, it is common practice to test smaller sample sizes. The ASTM packaging conditioning tests are shown… to be five-times stress tests.”

ln(1-C)/ln(R), where C = 0.95 and R = 0.95,

The exact number can be found by using the success run theorem. In our example, we estimate at least 95% reliability based on the 5% failures while using 5x stress test conditions, when compared to the original 1% failures.

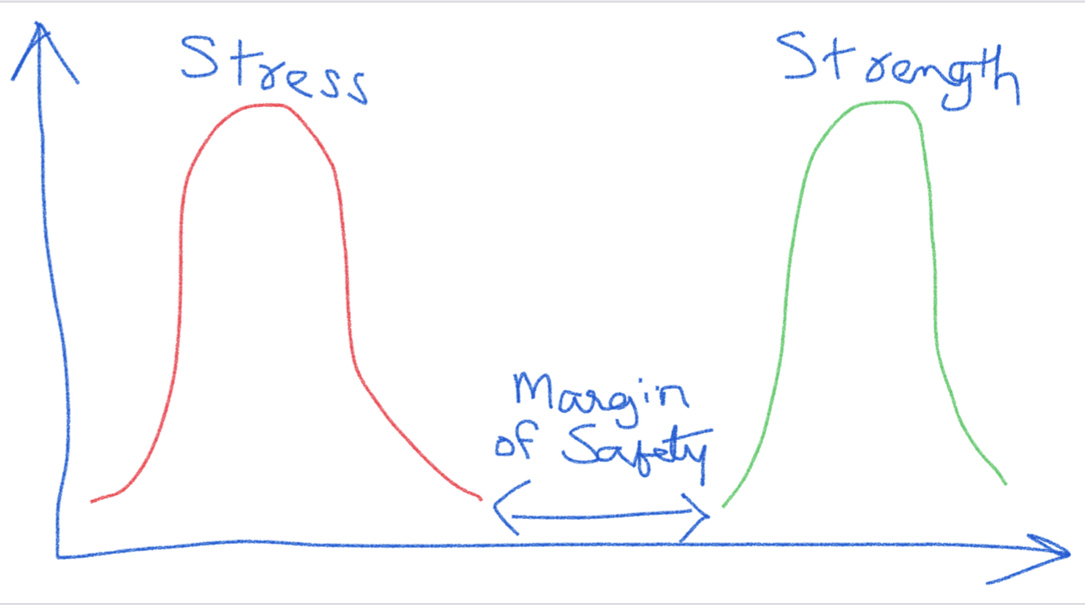
A common depiction of a stress/strength relationship is shown below for a product. We can see that as long as the stress distribution doesn’t overlap with the strength distribution, the product should function with no issues. The space between the two distributions is referred to as the margin of safety. Often, the product manufacturer defines the normal operating parameters based on this. The specifications for the product are also based on this, and some value of margin of safety is incorporated in the specifications.

“An attribute stress test results in a pass/fail result. However, the unit is exposed to higher stresses than are typical under normal conditions. As a result, the stress test is expected to produce more failures than will occur under normal conditions. This allows the number of units tested to be reduced. Stress testing requires identifying the appropriate stressor, including time, temperature, force, humidity, and voltage. Examples of stress tests include dropping a product from a higher height, exposing a product to more cycles, and exposing a product to a wider range of operating conditions.

n = ln(1 – C)/ ln(R), where n is the sample size, ln is the natural logarithm, C is the confidence level, and R is reliability.

Using the equation

The formula for the success run theorem is given as:

Always keep on learning.

Quality Digest does not charge readers for its content. We believe that industry news is important for you to do your job, and Quality Digest supports businesses of all types.

Published Oct. 1, 2023, in Harish’s Notebook.

It should be apparent that if the product is failing at the elevated stress level, we can’t claim the margin of safety we were going for. We must clearly understand how the product will be used in the field and what the normal performance conditions are. We need a good understanding of the safety margins involved. With this approach, if we’re able to improve the product design to maximize the safety margins for the specific attributes, we can then use a smaller sample size than what’s noted in the table above.

So please consider turning off your ad blocker for our site.

Selecting a sample size must be based on the risk involved. The specific combinations of reliability and confidence level should also be tied to the risk involved. Testing for higher-risk profile attributes requires higher sample sizes. For example, for a high-risk attribute, one can test 299 samples, and if there were no rejects found, then claim that at 95% confidence, the product lot is at least 99% conforming, or the process that produced the product is at least 99% reliable.

If we had started with a 95% reliability (5% failures utmost) and 95% confidence at the 1x stress conditions, and we go to 2x stress conditions, then we need to calculate the reduced sample size based on 10% failures (2 x 5%). This means that the reliability is estimated to be 90% at 2x stress conditions. Using 0.95 for confidence and 0.90 reliability, this equates to a reduced sample size of 29.

Lean

Using Stress/Strength Analysis to Reduce Sample Size

Practical suggestions for reducing sample sizes for attribute testing

The common way to select an appropriate sample size using reliability and confidence level is based on the success run theorem. The often-used sample sizes are shown below. The assumptions for using binomial distribution hold true here.

For example, let’s say that the maximum force that the glue joint of a medical device would see during normal use is 0.50 lb-force (lbf), and the specification is set as 1.5 lbf to account for a margin of safety. It is estimated that a maximum of 1% can likely fail at 1.5 lbf. This refers to 99% reliability. As part of design verification, we could test 299 samples at 1.5 lbf and if we do not have any failures, claim that the process is at least 99% reliable at 95% confidence level. If the glue joint is tested at 0.50 lbf, we should be expecting no product to fail. This is after all, the reason to include the margin of safety.

Today I’m looking at some practical suggestions for reducing sample sizes for attribute testing. A sample is chosen to represent a population. The sample size should be sufficient to represent the population parameters such as mean and standard deviation. Here, we’re looking at attribute testing, where a test results in either a pass or a fail.

Similarly, if we are to test the glue joint at 3 lbf (twofold), we will need 150 samples (half of 299 from the original study) with no failures to claim the same 99% reliability at 95% confidence level during the normal use of product. The rule of thumb is that when aiming for a testing margin of safety of x, we can reduce the sample size by a factor of 1/x while maintaining the same level of reliability and confidence.

Thanks,
Quality Digest

منبع: https://www.qualitydigest.com/inside/lean-article/using-stressstrength-analysis-reduce-sample-size-101623.html

However, someone has to pay for this content. And that’s where advertising comes in. Most people consider ads a nuisance, but they do serve a useful function besides allowing media companies to stay afloat. They keep you aware of new products and services relevant to your industry. All ads in Quality Digest apply directly to products and services that most of our readers need. You won’t see automobile or health supplement ads.